TL;DR
Chromosome – individual in population always represent a single problem solution. Binary chromosome is built of binary genes (0 or 1, true or false), this kind of representation make operators implementation much easier, but also has some disadvantages.
Why to bother ?
In the previous post I presented a Genetic Algorithm chromosomes operators. I made some assumptions there to make life easier and be able to show you how genetic operators work. Here, in the next step, I would like to show you alternative version of chromosome – other possible representation – binary one. That representation is very useful for small number of dimensions – for example 2D space. They are good choice when the chromosome numerical values are not huge integer numbers, or even floating point numbers but with smaller precision. The limitation is always a time used to calculate one GA loop (one generation).
I value examples over solid text, so I will do it this way.
Problem to solve
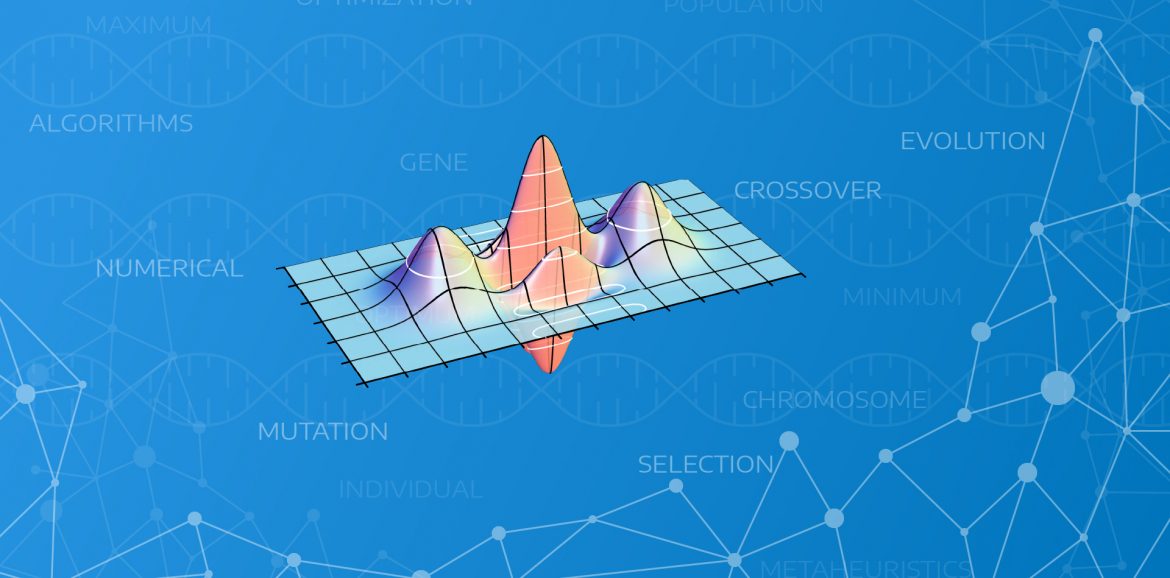
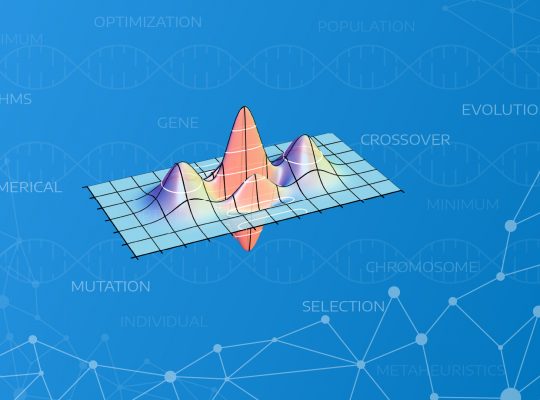
Let’s take an example function as our target:
\[ f(x,y)=x \cdot sin(y) + y \cdot sin(x) \]
I present below the visualization of the function to make it easier to understand:
As we can see we have here a space range:
\[ x \in \{ 0 \dots 8\}, y \in \{ 0 \dots 8\} \]
As we can see there is one global maximum in this space at \( (x,y) = (8, 8) \). This is the place which we will try to find using our genetic algorithm. To make the problem non trivial we can see that there are two other local maximums – that places will be some kind of obstacles: \( (x,y) = (2,8)\) and \((x,y) = (8,2) \).
Binary chromosome
We can define chromosome matching all criteria that we know:
- the genes should represent 2D space, so we will have x and y values – floating point numbers,
- the range of both variables is \( \{ 0 \dots 8\} \),
- we can assume some precision of \(x,y\) variables, to make it possible to represent them as binary strings. Let’s assume 3 the most significant digits as required precision.
Having these information we can calculate how many bits do we need to represent our numbers. The length of each range is 8.0, so we should create at least
\[ 8\cdot10^3=8000 \]
of the same sub ranges which digitize our space, additionally w can notice that
\[ 2^{12}<8000\leqslant 2^{13} . \]
This denotes for us that the smallest number of bits that will cover our space and precision is 13. We will use 13 bits for each variable then, so finally our chromosome will have 26 genes. First 13 will represent x, next 13 will represent y.

We need to define now how to calculate the x from binary representation. Let’s look on the chromosome like this:
\[ (10100101100110001100010111). \]
To decode it into values x and y we can to use following equations:
\[ x \in \left \{ x_1, x_2,…x_n \right \} (\mathrm{range}) \]
\[ y \in \left \{ y_1, y_2,…y_n \right \} (\mathrm{range}) \]
\[ n=N – 1 \]
\[ N – \textrm{number of genes representing single variable}\]
\[ x = x_1 + \frac{decimal(\textrm{genes representing x})\cdot (x_n – x_1)}{2^N – 1}\]
\[ y = y_1 + \frac{decimal(\textrm{genes representing y})\cdot (y_n – y_1)}{2^N – 1}\]
and using our real values we have:
\[ x = \frac{decimal(1010010110011_2) \cdot 8}{2^{13} – 1} = 4.791600537 \]
\[ y = \frac{decimal(0001100010111_2) \cdot 8}{2^{13} – 1} = 0.772555243 . \]
Changes in classic operators
Below I pointed in short, what changes we need to introduce to previously described operators from [2] Genetic Algorithms: Operators to make them work with binary chromosome representation.
Selection
The classic selection operator will not actually change, the only change is in evaluation of individual adaptation. We need to decode binary chromosome first into two floating point values, then we can calculate value of objective function \( f(x,y) \).
Crossover
Crossover changed a little bit, because we will not use floating point numbers anymore, now we use bit arrays, so we find a point of division in genes and exchange genetic material – bits between two chromosomes. The result may be outside the possible ranges. That is the risk of using number of bits that can cover bigger space than required. I explained a simple solution at the end.
Mutation
It will be no surprise, that we mutate single bit by changing it into 0 or 1 randomly. Mutation can result in exactly the same gene as before – that’s nothing strange here. But be aware that the chromosome created after mutation may be invalid (outside possible solutions space).
Outside the space ?
For binary chromosomes, we can have a situation mentioned before – the x or y value may be outside the available bounds – outside constraints. In such situation we can “adjust” the chromosome genes to make them fit back into the space. For example:
\[ \textrm{if }x < 0 \Rightarrow x=0 \]
\[ \textrm{if }x > 8.0 \Rightarrow x = 8.0 .\]
Same with y. This will prevent algorithm from generating invalid individuals.
Penalty function
Other way to handle invalid chromosomes is to create a penalty function, which will “penalize” the chromosome by changing evaluation value to be bed, to significantly or less significantly mark the chromosome as “bad one” 🙂
HINT: Sometimes invalid chromosomes are left in population to introduce some mechanisms of nature. This can led us to find very good solutions at the end, because we explore normally impossible to explore places.
That’s all about binary chromosomes in Genetic Algorithms. I know that we can always add more here, but the aim is to make it short and easy to everyone.
Thank you for reading.