[2] Genetic Algorithms: Operators

TL;DR

Every classic genetic algorithm is built from 4 basic phases: crossover (expanding the population), mutation, evaluation and selection repeated in loop. There are many other steps that can be added and variations, but the classic genetic algorithm contains only that four. I also explain a basic terms from GA world.

Please check short schema too understand how the genetic algorithms work:

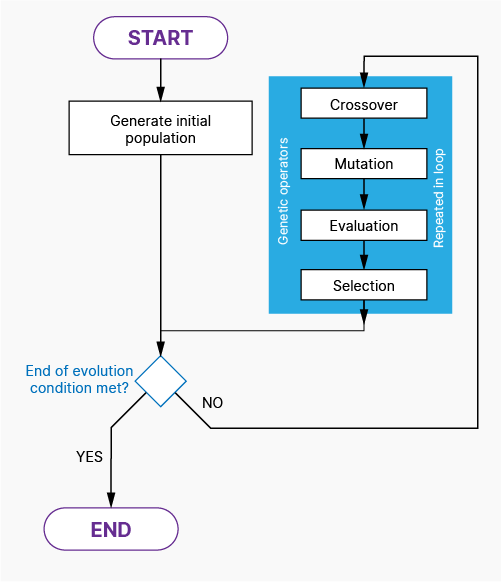
The full algorithm is build from following phases:

1. Generation – generate an initial population or generate missing individuals.
2. Crossover – make a mix of individuals, exchange individual “genetic code” to simulate natural processes.
3. Mutation – randomly change some of individuals to mimic real mutations which can be met in nature – evolution.
4. Evaluation – calculates the value denoting how good is each chromosome in population.
5. Selection – compares individuals in population, chooses only the best ones and trims the extended before population back to original size.

We can stop algorithm after the specific STOP criteria have been satisfied. Below some examples:

• Stop algorithm after fixed number of generations – populations.
• Stop algorithm when the best calculated evaluation is not changing with given precision. We define a value which denotes how precise should be the result e.g. 0.00001, to stop simulation when difference between previous the best individual and current the best individual is equal or lower than this value.

At the end, the best of all individuals that we found over the generations becomes our solution.

Now let’s make short intro to the GA (Genetic Algorithms) nomenclature.

Individual / Chromosome / Gene

In GA (genetic algorithms) the solutions of problem are called individuals and are presented in any arbitrary selected form.

Small digression. In real evolution, each individual in population is represented by it’s DNA (chromosomes). To make it easier to imagine and explain we can call individual a chromosome with a set of genes, but to be honest it is not the fully right term. Normally in nature we have individuals which have not one chromosome, but this terminology – chromosome and gene is very close to the reality we want to discuss. In my opinion it very good to describe algorithms and solution representations.

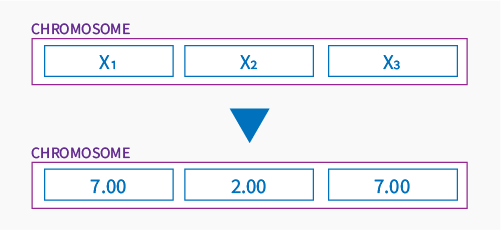
Continuing, each gene is a part of chromosome locating him in a space of all solutions of the problem. Let’s assume that chromosome is a point on a Google map, it could be represented (just for example) by two genes like below:

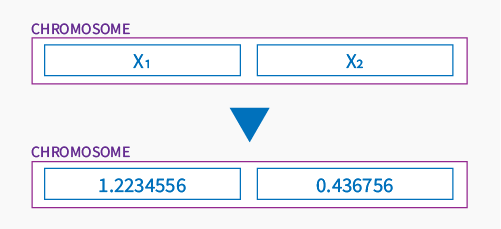
or by 3 in 3D space:

Population

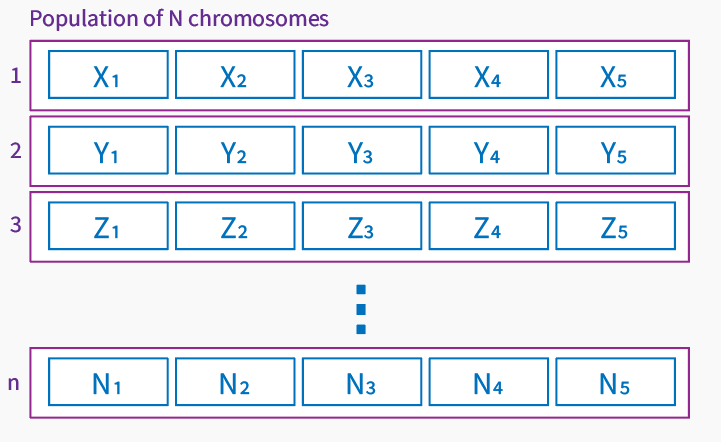
Population is a group of individuals leaving in the same environment – using optimization language – the same space of solutions. Population in our case is a set of chromosomes that creates a current space of found solutions. The size of population may vary for different problems that optimization is solving.

Operators: crossover (binary chromosomes)

The operator I want to describe now is crossover. Crossover is used to exchange the genetic material. In genetic terminology it is a breaking of chemical bonds and exchanging the parts between chromosomes. In our example the chemical bonds are rather virtual and we can locate them between genes in chromosome. For genetic algorithm this operator is used to create new children, and is based on so called crossover probability \( p_c \) which denotes the probability of selecting a particular chromosome to become a parent for next generation. Let’s take a look on the steps list:

1. Assume a probability value \( p_c = 0.25 \),
2. Find a random number in range \( rnd = 0 \dots 1 \),
3. If \( rnd < p_c \) then select for crossover as parent,
4. Make sure to have even number of parents, if not go through the population and find one more parent different than already selected (this condition may vary)
5. Pick a parents pair one by one from the collected list and perform crossover.
   • Pick a random number \(gene_{pos}\) which is always between two genes in chromosome (crossover point), from 1 to number of genes – 1
   • Create two child chromosomes
   • First by copying genes located on the left side from crossing point (from parent 1) and on the right side of crossing point (from parent 2)
   • Second by copying genes located on the left side from crossing point (from parent 2) and on the right side of crossing point (from parent 1)
6. Add new chromosome to the population (population size will be now bigger than normal)

Below you can see how one-point crossover works.

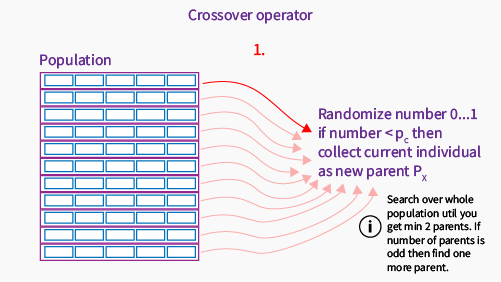
Explaining the first step: we go through the population and for each individual randomly pick a number between 0..1. If the number is less than our crossover probability, this individual will be a new parent. We always need to have even number of parents, but it depends on the crossover operator type.

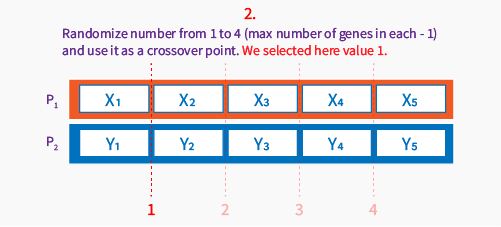
Then we select a point between genes to be a crossover point, for this operator (one point crossover) we skip first position and last position in chromosome, to be sure, we will always have at least one gene exchanged.

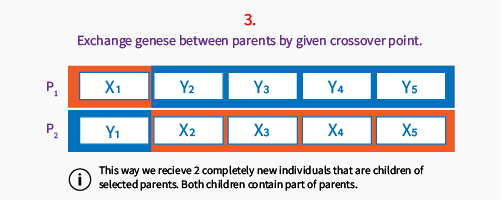
Crossover is very specific operator because in some cases it may generate invalid individuals – outside the solutions space or the ones that makes no sense from the perspective of problem we’re solving. Here we focus on simple binary chromosomes (genes are 0 or 1) or chromosomes that can be easily exchanged in parts giving valid individual as a result.

Operators: uniform mutation

In real live we can observe genetic mutation very often. Example, moles on the skin, but also more serious changes like genetic disease. Mutation introduces something new into chromosome, shows new way in an exploration space. Without mutation we would find easy solutions only, we won’t be able to find surprising solutions hidden somewhere. I will show you the simplest mutation – uniform mutation. How it works? It’s simple, we need to define the mutation probability first. A default value can be for us 25%, for computation it will be 0.25. Next step is to find one random gene within whole population, then we check if the gene should be mutated. There is a formula to check it:

1. Assume a probability value \( p_m = 0.25 \),
2. Find a random number in range \( rnd = 0 \dots 1 \),
3. If \( rnd < p_m \) then select this chromosome for mutation,
4. Pick a random integer number in range \( rnd_{int} = 0 \dots 5 \) (position of gene),
5. Mutate the gene using a random value for this gene.

And how to mutate the gene? We need to know the possible values range for gene, and simple randomize new gene in available range and replace it by this random value. This way we create a mutated gene. 

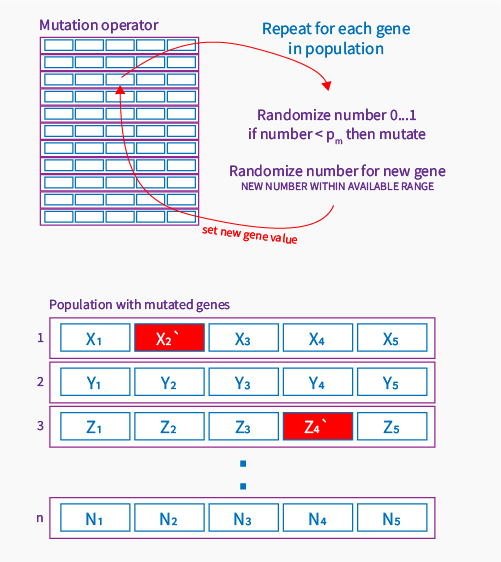
The chromosomes created this way, like before may be invalid, outside search space bounds or completely not real. This should be handled in selection or evaluation of chromosome.

NOTE: Please be aware that this is just a basic framework description. There exist many variations of mutation and even some of them create invalid genes which are outside the available range. That kind of mutations helps to find solutions that normally can be unreachable.

Operators: classic selection

Natural selection in real life denotes that only the strongest individuals can survive. The same idea was brought to the GA’s. The evaluation of chromosome fitness is a key. We always need to have evaluation function that will give us a number or a group of parameters saying that this individual is better than the other, or that the individual is invalid and should be eliminated as fast as possible (e.g. by penalty function that will be described in [4] Genetic Algorithms: simple code post of this series).

Let’s make an example. We define an objective function at first:

\[ f(x,y)=x \cdot sin(y) + y \cdot sin(x) \]

We want to find a maximum of that function in defined space (rectangle 8×8):

\[ x \in \{ 0 \dots 8\}, y \in \{ 0 \dots 8\}. \]

In this way, we will favor chromosomes that has bigger evaluation result of function \( f(x,y) \). We will maximize the function:

\[ eval(x,y)=max(f(x,y)). \]

How it works? We go through the population, calculating the value of function \( f(x,y) \) for each chromosome. 

The selection will simply sort whole population by the value of \( eval(x,y) \) function and remove all individuals that are “outside” population size. In that way we always eliminate the worst individuals. Easy, isn’t it? Yeah, but this is only one of possibilities and not the best solution, we can call it a classic selection. 

Other selection types

Imagine a fact that in real life all weak animals will always die. That’s how it may work in the simplest selection. We just choose the worse individuals and remove them – kill them. Normally selection is a very complex process in nature. To make the GA selection closer to it, a lot of variations of selection operator were created. It’s not in the scope of this post to describe them all, but take a look on some examples. Maybe it will be time to cover them in other posts from this series.

• Roulette wheel selection,
• Tournament selection,
• Elitist selection,
• Rank selection,
• Boltzman selection,
• … and many variations of them.

Summary

I tried to present you how the genetic algorithm operators works in the simplest words. In the next posts of this series I will explain how to encode the numeric solution / value in the chromosome using various representations.

Thank you for reading.